用 CVXPY 手搓一个 SVM
用 CVXPY 手搓一个 SVM
支持向量机(Support Vector Machine,SVM)是一种常用的机器学习算法,用于分类和回归问题。SVM的基本思想是寻找一个最优的超平面,将不同类别的数据样本分隔开来。设样本点为 $(x_i,y_i)(i = 1,\cdots,n)$ ,其中 $x_i\in \mathbb{R}^m $ ,标签 $y_i\in{1, -1}$ ,线性分类面方程为 $w^Tx + b = 0, w\in\mathbb{R}^m , b\in\mathbb{R}$ 。SVM希望找到超平面参数$w, b$,满足如下的优化问题
\[\min \frac{1}{2} w^Tw\] \[\text{s.t.} y_i(w^Tx_i + b) \geq 1\]这是一个凸的二次规划问题,因此一定有最优解。引入对偶变量 $\alpha_i\geq 0(i = 1,\cdots,n)$,拉格朗日函数为
\[L(w, b, \alpha) = \frac{1}{2} w^Tw - \sum_{i = 1}^n \alpha_i[y_i(w^Tx_i + b) - 1]\]KKT条件为
\[\nabla_w L(w, b, \alpha) = w - \sum_{i = 1}^n \alpha_iy_ix_i = 0\] \[\nabla_b L(w, b, \alpha) = -\sum_{i = 1}^n \alpha_iy_i = 0\] \[\alpha_i \geq 0\] \[\alpha_i[y_i(w^Tx_i + b) - 1] = 0\]将第一个KKT条件和第二个 KKT条件带入带入拉格朗日函数,我们就得到了对偶问题
\[\max Q(\alpha) = \sum_{i = 1}^n \alpha_i - \frac{1}{2}\sum_{i = 1}^n\sum_{j = 1}^n \alpha_i\alpha_jy_iy_jx_i^Tx_j\] \[\text{s.t.} \alpha_i \geq 0, \sum_{i = 1}^n \alpha_iy_i = 0\]这同样是一个凸的二次规划问题。理论上,我们可以通过求解对偶问题得到对偶变量 $\alpha$,将其带入KKT条件就可得到超平面的参数。同时根据第四个KKT条件,我们得到 $\alpha_i \neq 0$ 处 $y_i(w^Tx_i + b) = 1$。这些点恰好位于边界上,因此被称为支持向量。这也是该算法被称为支持向量机的原因。
CVXPY是一个用于凸优化问题建模和求解的Python库。它提供了一种简洁而直观的方式来描述凸优化问题,并使用底层求解器来求解这些问题。我们将用CVXPY实现SVM算法。
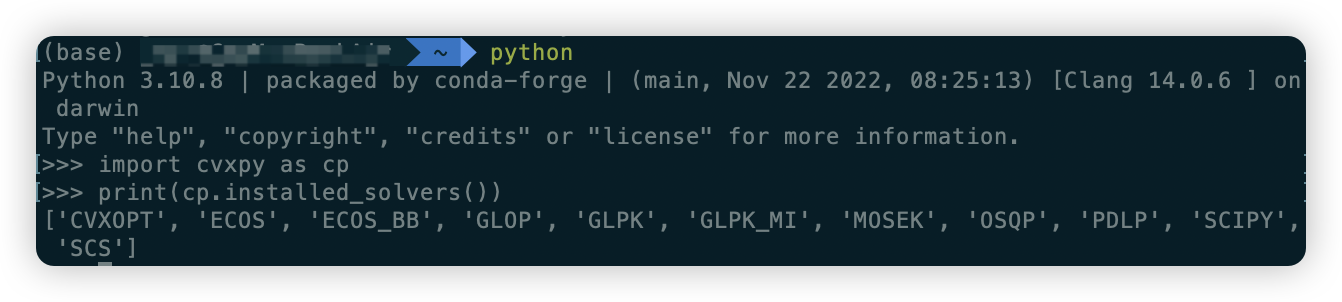
CVXPY的安装非常简单。首先确保电脑已配置Python环境。在终端中输入
1
pip install cvxpy
即可。进入Python Console,输入以下命令
1
2
import cvxpy as cp
print(cp.installed_solvers())
如果出现以下输出说明CVXPY安装成功。输出显示了已安装的求解器。
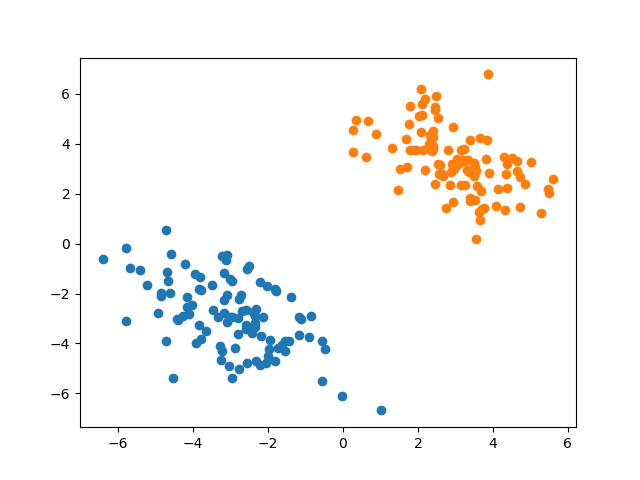
首先我们生成一组线性可分的数据。从均值为 $\begin{bmatrix} -3 \ -3 \ \end{bmatrix}$,协方差矩阵为 $\begin{bmatrix} 2 & -1 \ -1 & 2 \ \end{bmatrix}$的二元正态分布中抽取100个样本作为正例,从均值为 $\begin{bmatrix} 3 \ 3 \ \end{bmatrix}$,协方差矩阵为 $\begin{bmatrix} 2 & -1 \ -1 & 2 \ \end{bmatrix}$的二元正态分布中抽取100个样本作为负例。核心代码如下。
1
2
3
4
5
6
7
8
9
10
def load_data():
mean1 = [-3, -3]
sigma1 = [[2, -1], [-1, 2]]
mean2 = [3, 3]
sigma2 = [[2, -1], [-1, 2]]
X1 = np.random.multivariate_normal(mean1, sigma1, 100)
X2 = np.random.multivariate_normal(mean2, sigma2, 100)
X = np.vstack((X1, X2))
y = np.hstack((np.ones(100), -np.ones(100)))
return X, y
画出散点图如下。可见样本点线性可分。
接下来我们进行数据的拟合。为了统一运算,对负例样本乘 -1。设样本矩阵 $X = [x_1, \cdots, x_n]^T$,全一向量 $1_n = [1, \cdots, 1]^T$ ,则对偶问题$Q(\alpha)$的优化目标可写作
\[1_n^T\alpha - \frac{1}{2}(X^T\alpha)^T(X^T\alpha)\]然后定义优化目标和约束,调用CVXOPT求解器进行求解。核心代码如下。
1
2
3
4
5
6
7
8
9
10
def fit(X, y):
x = X.copy()
x[y == -1, :] = -x[y == -1, :]
n = x.shape[0]
alpha = cp.Variable(n)
objective = cp.Minimize(0.5 * cp.sum_squares(x.T @ alpha) - np.ones(n) @ alpha)
constraint = [alpha >= 0, y @ alpha == 0]
prob = cp.Problem(objective, constraint)
prob.solve(solver='CVXOPT')
print(f"dual variable = {alpha.value}")
得到对偶变量的最优解后,代入第一个KKT条件可以计算出 $w$。 $\alpha_i \neq 0$的对偶变量对应了支持向量。代入支持向量满足的边界方程可以计算出 $b$。核心代码如下。
1
2
3
4
5
w = x.T @ alpha.value
index = np.where(abs(alpha.value) > 1e-3)[0]
print(f"support vector index = {index}")
b = np.mean(y[index] - X[index, :] @ w)
return w, b, index
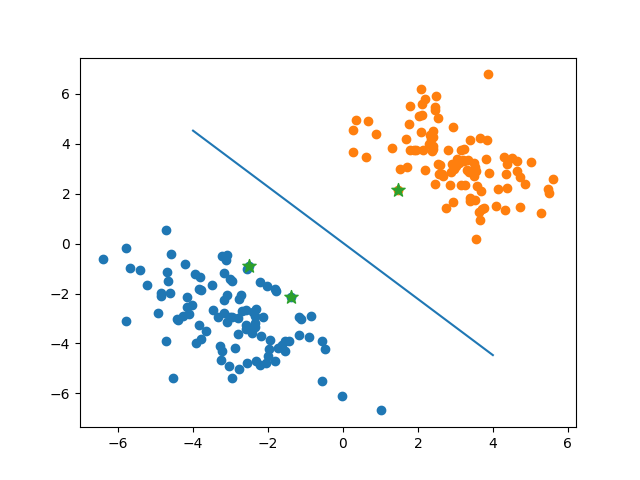
程序运行结果如下。可见有3个支持向量。其余的对偶变量非常接近0。
1
2
3
4
dual variable = [ 1.43531769e-09 3.28358675e-11 -4.70081346e-11 ... -1.23193041e-12
1.46991949e-11 -4.72866927e-11]
support vector index = [ 11 42 111]
w = [-0.30023937 -0.26737101], b = 0.007281446816055766
将分界面和支持向量可视化,可见SVM确实找到了最优分类面。
附程序完整代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import numpy as np
from matplotlib import pyplot as plt
import cvxpy as cp
def load_data():
mean1 = [-3, -3]
sigma1 = [[2, -1], [-1, 2]]
mean2 = [3, 3]
sigma2 = [[2, -1], [-1, 2]]
X1 = np.random.multivariate_normal(mean1, sigma1, 100)
X2 = np.random.multivariate_normal(mean2, sigma2, 100)
X = np.vstack((X1, X2))
y = np.hstack((np.ones(100), -np.ones(100)))
return X, y
def fit(X, y):
x = X.copy()
x[y == -1, :] = -x[y == -1, :]
n = x.shape[0]
alpha = cp.Variable(n)
objective = cp.Minimize(0.5 * cp.sum_squares(x.T @ alpha) - np.ones(n) @ alpha)
constraint = [alpha >= 0, y @ alpha == 0]
prob = cp.Problem(objective, constraint)
prob.solve(solver='CVXOPT')
print(f"dual variable = {alpha.value}")
w = x.T @ alpha.value
index = np.where(abs(alpha.value) > 1e-3)[0]
print(f"support vector index = {index}")
b = np.mean(y[index] - X[index, :] @ w)
return w, b, index
if __name__=="__main__":
X, y = load_data()
w, b, index = fit(X, y)
print(f"w = {w}, b = {b}")
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.scatter(X[y == -1, 0], X[y == -1, 1])
plt.scatter(X[index, 0], X[index, 1], marker='*', s=100)
plt.plot((-4, 4), ((-b + 4 * w[0]) / w[1], (-b - 4 * w[0]) / w[1]))
plt.show()