用 CVXOPT 手动实现一个线性软间隔 SVM
支持向量机(Support Vector Machine,SVM)是一种常用的机器学习算法,用于分类和回归问题。SVM的基本思想是寻找一个最优的超平面,将不同类别的数据样本分隔开来。设样本点为 $(\mathbf{x}_i,y_i)(i = 1,\cdots,N)$ ,其中 $\mathbf{x}_i\in \mathbb{R}^m $ ,标签 $y_i\in\{1, -1\}$ ,线性分类面方程为 $\mathbf{w}^T\mathbf{x} + b = 0, \mathbf{w}\in\mathbb{R}^m , b\in\mathbb{R}$ 。SVM希望找到超平面参数$\mathbf{w}, b$,满足如下的优化问题
\[\min_{\mathbf{w}} \frac{1}{2} \|\mathbf{w}\|^2 + C\sum_{i = 1}^N \xi_i\] \[\text{s.t.}\quad y_i(\mathbf{w}^T\mathbf{x}_i + b) \geq 1 - \xi_i, \quad \xi_i \geq 0, \quad i = 1, \cdots, N\]这是一个线性约束下的凸二次规划问题。
1. 对偶问题的数学形式
引入对偶变量 $\alpha_i\geq 0, r_i\geq 0(i = 1,\cdots,N)$,拉格朗日函数为
\[L(\mathbf{w}, b, \mathbf{\xi}, \boldsymbol{\alpha}, \mathbf{r}) = \frac{1}{2} \|\mathbf{w}\|^2 + C\sum_{i = 1}^N \xi_i - \sum_{i = 1}^N \alpha_i[y_i(\mathbf{w}^T\mathbf{x}_i + b) - 1 + \xi_i] - \sum_{i = 1}^N r_i\xi_i\]KKT条件为
\[\nabla_\mathbf{w} L(\mathbf{w}, b, \mathbf{\xi}, \boldsymbol{\alpha}, \mathbf{r}) = \mathbf{w} - \sum_{i = 1}^n \alpha_iy_i\mathbf{x_i} = 0\] \[\nabla_b L(\mathbf{w}, b, \mathbf{\xi}, \boldsymbol{\alpha}, \mathbf{r}) = -\sum_{i = 1}^N\alpha_i y_i = 0\] \[\nabla_{\xi_i} L(\mathbf{w}, b, \mathbf{\xi}, \boldsymbol{\alpha}, \mathbf{r}) = C - \alpha_i - r_i = 0\]整理可得对偶问题的形式为
\[\begin{aligned} \max_{\alpha} \quad & \sum_{i=1}^{N} \alpha_i - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j \\ \text{s.t.} \quad & 0 \leq \alpha_i \leq C \quad \text{for } i = 1, \dots, N \\ & \sum_{i=1}^{N} \alpha_i y_i = 0 \end{aligned}\]写成最小化的形式为
\[\begin{aligned} \min_{\alpha} \quad & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j - \sum_{i=1}^{N} \alpha_i \\ \text{s.t.} \quad & 0 \leq \alpha_i \leq C \quad \text{for } i = 1, \dots, N \\ & \sum_{i=1}^{N} \alpha_i y_i = 0 \end{aligned}\]其中:
$N$ 是样本数量。
$\alpha_i$ 是每个样本对应的拉格朗日乘子,这是我们要求解的变量。
$y_i \in \{-1, 1\}$ 是样本 $i$ 的类别标签。
$\mathbf{x}_i$ 是样本 $i$ 的特征向量。
$C > 0$ 是惩罚参数,控制对误分类的惩罚程度。
对偶问题是一个标准的凸二次规划(QP)问题。其目标函数是关于拉格朗日乘子 $\boldsymbol{\alpha}$ 的二次函数,约束是线性的。
2. 转换为QP标准形式
CVXOPT 是一款基于 Python 的凸优化软件包,支持密集和稀疏矩阵运算,支持线性规划、二次规划和锥优化等问题。CVXOPT 的安装非常简单,通过 pip install cvxopt 或者 conda install cvxopt -c conda-forge 即可安装。其用来求解 QP 问题的标准形式为:
其中$P$ 是一个正定矩阵,$G \mathbf{x} \leq h$ 表示一组不等式约束,$A \mathbf{x} = b$ 表示一组等式约束。因此我们可以将 SVM 的对偶问题写成 QP 标准形式:
变量向量:$\mathbf{x} \leftarrow \boldsymbol{\alpha} = [\alpha_1, \alpha_2, …, \alpha_N]^T$
二次项矩阵 (P):$P_{ij} = y_i y_j \mathbf{x}_i^T \mathbf{x}_j$,写成矩阵形式就是 $P = (yy^T)\odot (X X^T)$
线性项向量 (q):$\mathbf{q} = [-1, -1, …, -1]^T$
等式约束:$\sum_{i=1}^{N} \alpha_i y_i = 0$ 对应 $A \boldsymbol{\alpha} = b$,其中 $A = [y_1, y_2, …, y_N]$,$b = 0$。
不等式约束:$\begin{bmatrix} -I_N \ I_N \end{bmatrix} \boldsymbol{\alpha} \leq \begin{bmatrix} 0 \ C \end{bmatrix}$,其中 $I_N$ 是 $N \times N$ 单位矩阵。上半部分表示了 $ \alpha_i \geq 0$,下半部分表示了 $\alpha_i \leq C$。
我们将这些参数传入 cvxopt.solvers.qp 函数,即可求解出 $\boldsymbol{\alpha}$。
3. 权重和偏置的求解
求解出 $\boldsymbol{\alpha}$ 后,我们可以利用 KKT 条件恢复权重和偏置。
权重 $\mathbf{w}$:根据公式 $\mathbf{w} = \sum_{i=1}^{N} \alpha_i y_i \mathbf{x}_i$ 计算。注意,只有 $\alpha_i > 0$ 的样本(支持向量)才对 $\mathbf{w}$ 有贡献。可以取阈值 1e-5,用于过滤掉数值上为零的 $\alpha_i$。
偏置 $b$:根据 KKT 条件,对于支持向量,有 $y_i (\mathbf{w}^T \mathbf{x}_i + b) = 1$。因此 $b = y_i - \mathbf{w}^T \mathbf{x}_i$。为了更鲁棒,我们对所有支持向量计算 $b$ 并取平均值。
据此我们可以定义一个MySVM类如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
class MySVM:
"""
利用CVXOPT求解线性SVM的对偶问题,实现一个简易的SVM类。
"""
def __init__(self, C=1.0):
"""
初始化SVM类。
参数:
C (float): 惩罚参数。
"""
self.C = C
self.w = None
self.b = None
self.alphas = None
def fit(self, X, y):
"""
训练SVM模型。
参数:
X (np.ndarray): 训练数据的特征矩阵,形状为 (N, D)。
y (np.ndarray): 训练数据的标签,形状为 (N,),值为 -1 或 1。
"""
N, D = X.shape
# 1. 构造QP问题的矩阵
y_outer = np.outer(y, y)
X_inner = X @ X.T
Q = matrix(y_outer * X_inner)
p = matrix(-np.ones(N))
A = matrix(y.reshape(1, -1), (1, N), 'd')
b = matrix(0.0)
G = matrix(np.vstack((-np.eye(N), np.eye(N))))
h = matrix(np.hstack((np.zeros(N), self.C * np.ones(N))))
# 2. 求解QP问题
solvers.options['show_progress'] = False # 关闭求解器输出
solution = solvers.qp(Q, p, G, h, A, b)
alphas = np.ravel(solution['x'])
# 3. 只对支持向量 (alpha_i > 0) 进行计算
alphas[alphas < 1e-5] = 0
sv_indices = (alphas != 0)
w = ((alphas[sv_indices] * y[sv_indices])[:, None] * X[sv_indices]).sum(axis=0)
# 4. 计算偏置 b(对所有支持向量求均值提高数值稳定性)
b_values = y[sv_indices] - X[sv_indices] @ w
b = np.mean(b_values)
# 5. 保存参数
self.w = w
self.b = b
self.alphas = alphas
def predict(self, X):
"""
对输入样本进行预测。
参数:
X (np.ndarray): 数据特征矩阵,形状为 (M, D)。
返回:
y_pred (np.ndarray): 预测标签,形状为 (M,)
"""
return np.sign(X @ self.w + self.b)
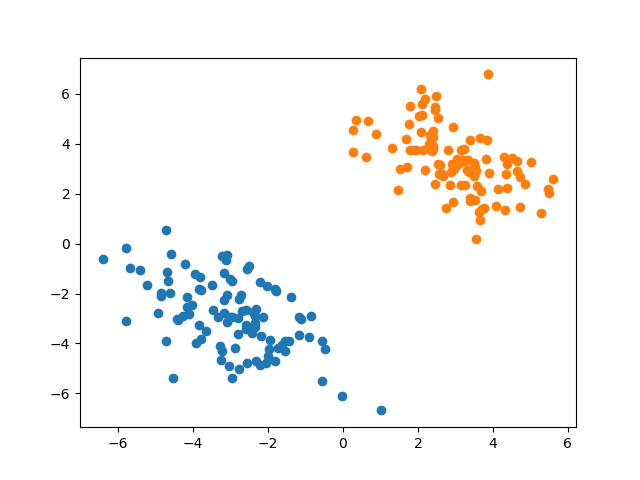
我们从均值为 $\begin{bmatrix} -3 \ -3 \ \end{bmatrix}$,协方差矩阵为 $\begin{bmatrix} 2 & -1 \ -1 & 2 \ \end{bmatrix}$的二元正态分布中抽取100个样本作为正例,从均值为 $\begin{bmatrix} 3 \ 3 \ \end{bmatrix}$,协方差矩阵为 $\begin{bmatrix} 2 & -1 \ -1 & 2 \ \end{bmatrix}$的二元正态分布中抽取100个样本作为负例。核心代码如下。
1
2
3
4
5
6
7
8
9
10
def load_data():
mean1 = [-3, -3]
sigma1 = [[2, -1], [-1, 2]]
mean2 = [3, 3]
sigma2 = [[2, -1], [-1, 2]]
X1 = np.random.multivariate_normal(mean1, sigma1, 100)
X2 = np.random.multivariate_normal(mean2, sigma2, 100)
X = np.vstack((X1, X2))
y = np.hstack((np.ones(100), -np.ones(100)))
return X, y
画出散点图如下。
使用手动实现的 SVM 进行训练,运行结果如下。可见有3个支持向量。其余的对偶变量非常接近0。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
alpha = [0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0.18555126 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0.18555127 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. ]
w = [-0.46540765 -0.39306261]
b = -0.052583387326479166
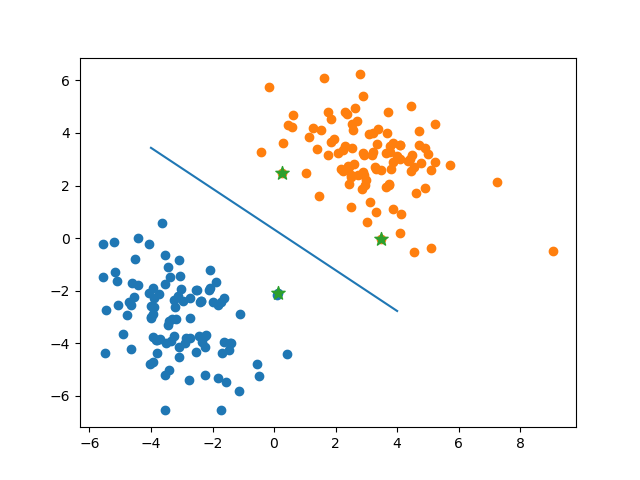
将分界面和支持向量可视化,可见SVM确实找到了最优分类面。
附程序完整代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
import numpy as np
from cvxopt import matrix, solvers
from matplotlib import pyplot as plt
class MySVM:
"""
利用CVXOPT求解线性SVM的对偶问题,实现一个简易的SVM类。
"""
def __init__(self, C=1.0):
"""
初始化SVM类。
参数:
C (float): 惩罚参数。
"""
self.C = C
self.w = None
self.b = None
self.alphas = None
def fit(self, X, y):
"""
训练SVM模型。
参数:
X (np.ndarray): 训练数据的特征矩阵,形状为 (N, D)。
y (np.ndarray): 训练数据的标签,形状为 (N,),值为 -1 或 1。
"""
N, D = X.shape
# 1. 构造QP问题的矩阵
y_outer = np.outer(y, y)
X_inner = X @ X.T
Q = matrix(y_outer * X_inner)
p = matrix(-np.ones(N))
A = matrix(y.reshape(1, -1), (1, N), 'd')
b = matrix(0.0)
G = matrix(np.vstack((-np.eye(N), np.eye(N))))
h = matrix(np.hstack((np.zeros(N), self.C * np.ones(N))))
# 2. 求解QP问题
solvers.options['show_progress'] = False # 关闭求解器输出
solution = solvers.qp(Q, p, G, h, A, b)
alphas = np.ravel(solution['x'])
# 3. 只对支持向量 (alpha_i > 0) 进行计算
alphas[alphas < 1e-5] = 0
sv_indices = (alphas != 0)
w = ((alphas[sv_indices] * y[sv_indices])[:, None] * X[sv_indices]).sum(axis=0)
# 4. 计算偏置 b(对所有支持向量求均值提高数值稳定性)
b_values = y[sv_indices] - X[sv_indices] @ w
b = np.mean(b_values)
# 5. 保存参数
self.w = w
self.b = b
self.alphas = alphas
def predict(self, X):
"""
对输入样本进行预测。
参数:
X (np.ndarray): 数据特征矩阵,形状为 (M, D)。
返回:
y_pred (np.ndarray): 预测标签,形状为 (M,)
"""
return np.sign(X @ self.w + self.b)
def load_data():
mean1 = [-3, -3]
sigma1 = [[2, -1], [-1, 2]]
mean2 = [3, 3]
sigma2 = [[2, -1], [-1, 2]]
X1 = np.random.multivariate_normal(mean1, sigma1, 100)
X2 = np.random.multivariate_normal(mean2, sigma2, 100)
X = np.vstack((X1, X2))
y = np.hstack((np.ones(100), -np.ones(100)))
return X, y
if __name__ == "__main__":
X, y = load_data()
model = MySVM()
model.fit(X, y)
print("alpha = ", model.alphas, "\nw = ", model.w, "\nb = ", model.b)
plt.scatter(X[y == 1, 0], X[y == 1, 1])
plt.scatter(X[y == -1, 0], X[y == -1, 1])
plt.scatter(X[model.alphas != 0, 0], X[model.alphas != 0, 1], marker='*', s=100)
plt.plot((-4, 4), ((-model.b + 4 * model.w[0]) / model.w[1], (-model.b - 4 * model.w[0]) / model.w[1]))
plt.show()
需要指出两点。首先,我们将 X @ X.T 替换为核函数矩阵 $K(\mathbf{x}_i, \mathbf{x}_j)$,即可轻松扩展到非线性SVM。例如,RBF核:K = np.exp(-gamma * np.sum((X[:, None] - X[None, :])**2, axis=-1))。其次,这个只是对 SVM 的一个简单实现,对于大规模数据集,通用的QP求解器(如CVXOPT)会变慢。scikit-learn 中的 SVC 是基于专门为 SVM 设计的序列最小优化(SMO)算法实现的,这里实践的目的是为了更好的理解 SVM 的原理。
本文总阅读量次