不只调用API:深度解析与手撸常见优化算法
在深度学习领域,优化器是必不可少的组件。深度学习将分类或回归问题建模成一个优化问题,而优化器负责调整模型的内部参数(如权重和偏置),以最小化损失函数。这个过程就像是登山者在迷雾中寻找山谷的最低点,而优化器就是为登山者提供方向和步幅的向导。一个好的优化器能够帮助模型更快、更稳定地收敛,找到一个更好的参数组合,从而提升模型的性能。从基础的梯度下降到更复杂的Adam和RMSProp,优化器是模型训练成功的关键,它决定了模型学习的效率和最终的预测精度。
通常情况下,我们只需调用 torch.optim 模块中的优化器即可轻松完成训练。例如,torch.optim.Adam 几乎可以解决大多数问题,但如果能自己手动实现这些优化器,可以极大地加深对它们的理解。手动实现优化器能让你从数学公式层面去剖析其工作原理,理解动量、自适应学习率等核心概念是如何通过代码被转化为实际的参数更新。这个过程不仅能让你更好地掌握每个优化器的特性和适用场景,还能在遇到模型收敛困难时,帮助你更精准地排查问题。接下来,我们将一步步手动实现从梯度下降到的Adam算法,深入剖析动量、Nesterov、Adagrad和RMSProp等核心优化算法的实现细节。
一、梯度下降(GD)
梯度下降是深度学习领域最简单也是使用最普遍的算法之一,它通过沿着函数最陡峭的下降方向(即梯度的负方向)迈出一步,逐步逼近函数的最小值。用公式表示就是
\[x_{t+1} \leftarrow x_t - \eta \nabla_x L(x_t)\]在Pytorch中,函数对变量的梯度可以通过函数的backward()方法进行反向传播,计算出的梯度保存在变量的grad属性中。因此我们可以定义一个GD类,其中step()方法进行一次梯度下降(注意需要torch.no_grad()避免自减过程中更新动态计算图导致死循环),zero_grad()方法将变量的梯度置0,为下一次迭代做准备。代码如下。
class GD:
def __init__(self, x, lr=0.01):
self.x = x
self.lr = lr
def step(self):
with torch.no_grad():
self.x -= self.lr * self.x.grad
def zero_grad(self):
self.x.grad.zero_()
二、带动量的梯度下降(MomentumGD)
标准的梯度下降容易实现且效果较好。然而,标准梯度下降有一个明显的缺点:它的每一步更新都只取决于当前位置的梯度,缺乏对过往移动方向的“记忆”,这在优化过程中容易产生不必要的震荡。为了保留历史信息,可以引入一个“动量”项,根据当前位置的梯度更新“动量”项,从而在加速收敛的同时,减少震荡并帮助算法更平稳地通过平坦区域。用公式表示就是
\[v_{t+1} \leftarrow \mu v_{t} + \nabla_x L(x_t)\] \[x_{t+1} \leftarrow x_t - \eta v_{t+1}\]这里“动量”项的更新采用了指数滑动平均的形式,可以使算法能够抛弃那些非常久远的梯度,保留较近的梯度信息。代码如下。
class MomentumGD:
def __init__(self, x, lr=0.01, momentum=0.9):
self.x = x
self.lr = lr
self.momentum = momentum
self.v = torch.zeros_like(x)
def step(self):
with torch.no_grad():
self.v = self.momentum * self.v + self.x.grad
self.x -= self.lr * self.v
def zero_grad(self):
self.x.grad.zero_()
三、Nesterov梯度下降(Nesterov GD)
和带动量的梯度下降类似,第一类Nesterov梯度下降也是通过引入“动量”项减小震荡、加速收敛。但不同的是Nesterov使用的是超前点处的梯度计算动量,具有前瞻性,通常比动量法收敛得更快。用公式表示就是
\[v_{t+1} \leftarrow \mu v_t + \nabla_x L(x_t - \eta\mu v_t)\] \[x_{t+1} \leftarrow x_t - \eta v_{t+1}\]但是如果按照这个公式进行实现,超前点处的梯度需要重新计算,带来了不必要的计算开销。因此我们令\(x_t' = x_t - \eta\mu v_t\),这样第二个迭代可以写为
\[\begin{aligned} x'_{t+1} &= x_{t+1} - \eta\mu v_{t+1} \\ &= x_t - \eta v_{t+1} - \eta\mu v_{t+1} \\ &= x_t' - \eta v_{t+1} + \eta\mu v_t - \eta\mu v_{t+1} \\ &= x_t' - \eta \nabla_xL(x_t') - \eta\mu v_{t+1} \end{aligned}\]因此第一类Nesterov梯度下降可以等价表示为
\[v_{t+1} \leftarrow \mu v_t + \nabla_x L(x_t')\] \[x_{t+1}' \leftarrow x_t' - \eta (\nabla_x L(x_t') + \mu v_{t+1})\]相当于我们更新的是超前点处的位置,而更新的方向是当前位置的梯度方向与动量方向的线性组合。事实上,PyTorch中的原生Nesterov梯度下降也是这么实现的。据此,我们可以写出如下代码。
class NesterovGD:
def __init__(self, x, lr=0.01, momentum=0.9):
self.x = x
self.lr = lr
self.momentum = momentum
self.v = torch.zeros_like(x)
def step(self):
with torch.no_grad():
self.v = self.momentum * self.v + self.x.grad
self.x -= self.lr * (self.x.grad + self.momentum * self.v)
def zero_grad(self):
self.x.grad.zero_()
四、AdaGrad
MomentumGD、NesterovGD解决了梯度下降只依赖当前位置处的梯度信息的问题。但梯度下降还有另一个问题:所有维度的学习率都是一样的。但不同维度由于取值范围的不同,其梯度可能存在数量级上的差异,收敛速率也会不同,从而产生某一维度接近收敛而另一维度远远没有收敛的情况。AdaGrad算法解决了这一问题:每个参数的当前学习率与其过去所有梯度平方之和的平方根成反比。关于损失函数有较大偏导的参数,其学习率会有较大的衰减;而偏导数较小的参数的学习率变化相对较小。换句话说,AdaGrad对每个维度的梯度进行了尺度变换,使得不同维度间的梯度大小是可比拟的。用公式表示就是
\[x_{t+1} \leftarrow x_t - \eta \frac{1}{\sqrt{\sum_{i = 1}^t (\nabla_x L(x_i))^2} + \epsilon}\odot \nabla_x L(x_t)\]这里向量间乘法是逐元素(element-wise)进行的,\(\epsilon = 10^{-8}\)防止除0。具体实现时,我们可以维护一个变量\(h_t\)储存过去所有梯度的平方和,这样迭代公式就可以写为
\[h_{t+1} \leftarrow h_t + (\nabla_x L(x_t))^2\] \[x_{t+1} \leftarrow x_t - \eta \frac{1}{\sqrt{h_{t+1}} + \epsilon} \odot \nabla_x L(x_t)\]代码如下。
class AdaGrad:
def __init__(self, x, lr=0.01, eps=1e-8):
self.x = x
self.lr = lr
self.h = torch.zeros_like(x)
self.eps = eps
def step(self):
with torch.no_grad():
self.h += self.x.grad ** 2
self.x -= self.lr * self.x.grad / (self.h ** 0.5+ self.eps)
def zero_grad(self):
self.x.grad.zero_()
五、RMSProp
与Adagrad类似,RMSProp也解决了自适应学习率的问题。但RMSProp将 AdaGrad 中的累计平方梯度变为指数滑动平均的形式。指数滑动平均方式使得算法能够抛弃那些非常久远的梯度, 使得算法的收敛速度更快。用公式表示就是
\[h_{t+1} \leftarrow \alpha h_t + (1 - \alpha)(\nabla_x L(x_t))^2\] \[x_{t+1} \leftarrow x_t - \eta \frac{1}{\sqrt{h_{t+1}} + \epsilon} \odot \nabla_x L(x_t)\]代码如下
class RMSProp:
def __init__(self, x, lr=0.01, alpha=0.9, eps=1e-8):
self.x = x
self.lr = lr
self.h = torch.zeros_like(x)
self.alpha = alpha
self.eps = eps
def step(self):
with torch.no_grad():
self.h = self.alpha * self.h + (1 - self.alpha) * self.x.grad ** 2
self.x -= self.lr * self.x.grad / (self.h + self.eps) ** 0.5
def zero_grad(self):
self.x.grad.zero_()
六、Adam
Adam 算法可以被看作是Momentum和RMSProp两种优化算法的集大成者。它在训练过程中,维护并更新两个指数移动平均值:
- 一阶矩估计(\(v_t\)):这是梯度的指数移动平均,类似于 Momentum 中的动量项。它决定了参数更新的方向,使得更新具有“惯性”,能够有效减少震荡并加速收敛。
- 二阶矩估计(\(h_t\)):这是梯度平方的指数移动平均,类似于 RMSProp。它通过梯度的平方来为每个参数创建一个自适应的学习率,确保频繁更新的参数学习率不会过高,而稀疏更新的参数也能得到有效学习。
Adam 的核心优势在于,它同时利用了梯度的一阶信息和二阶信息。它既有 Momentum 算法的平滑和加速效果,又有 RMSProp 的自适应学习率能力,从而在大多数深度学习任务中表现出极佳的稳定性和收敛速度。因此,它成为了目前最常用、最稳定的默认优化器之一。用公式表示就是
\[t \leftarrow t+1\] \[v_{t+1} \leftarrow \beta_1 v_t + (1 - \beta_1)\nabla_x L(x_t)\] \[h_{t+1} \leftarrow \beta_2 h_t + (1 - \beta_2)(\nabla_x L(x_t))^2\] \[\hat{v}_{t+1} \leftarrow \frac {v_{t+1}}{1 - \beta_1^t}\] \[\hat{h}_{t+1} \leftarrow \frac {h_{t+1}}{1 - \beta_2^t}\] \[x_{t+1} \leftarrow x_t - \eta \frac{1}{\sqrt{\hat{h}_{t+1}} + \epsilon} \odot \hat{v}_{t+1}\]代码如下。
class Adam:
def __init__(self, x, lr=0.01, beta1=0.9, beta2=0.999, eps=1e-8):
self.x = x
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.eps = eps
self.v = torch.zeros_like(x)
self.h = torch.zeros_like(x)
self.t = 0
def step(self):
self.t += 1
with torch.no_grad():
self.v = self.beta1 * self.v + (1 - self.beta1) * self.x.grad
self.h = self.beta2 * self.h + (1 - self.beta2) * self.x.grad ** 2
v_hat = self.v / (1 - self.beta1 ** self.t)
h_hat = self.h / (1 - self.beta2 ** self.t)
self.x -= self.lr * v_hat / (h_hat.sqrt() + self.eps)
def zero_grad(self):
self.x.grad.zero_()
七、算法测试
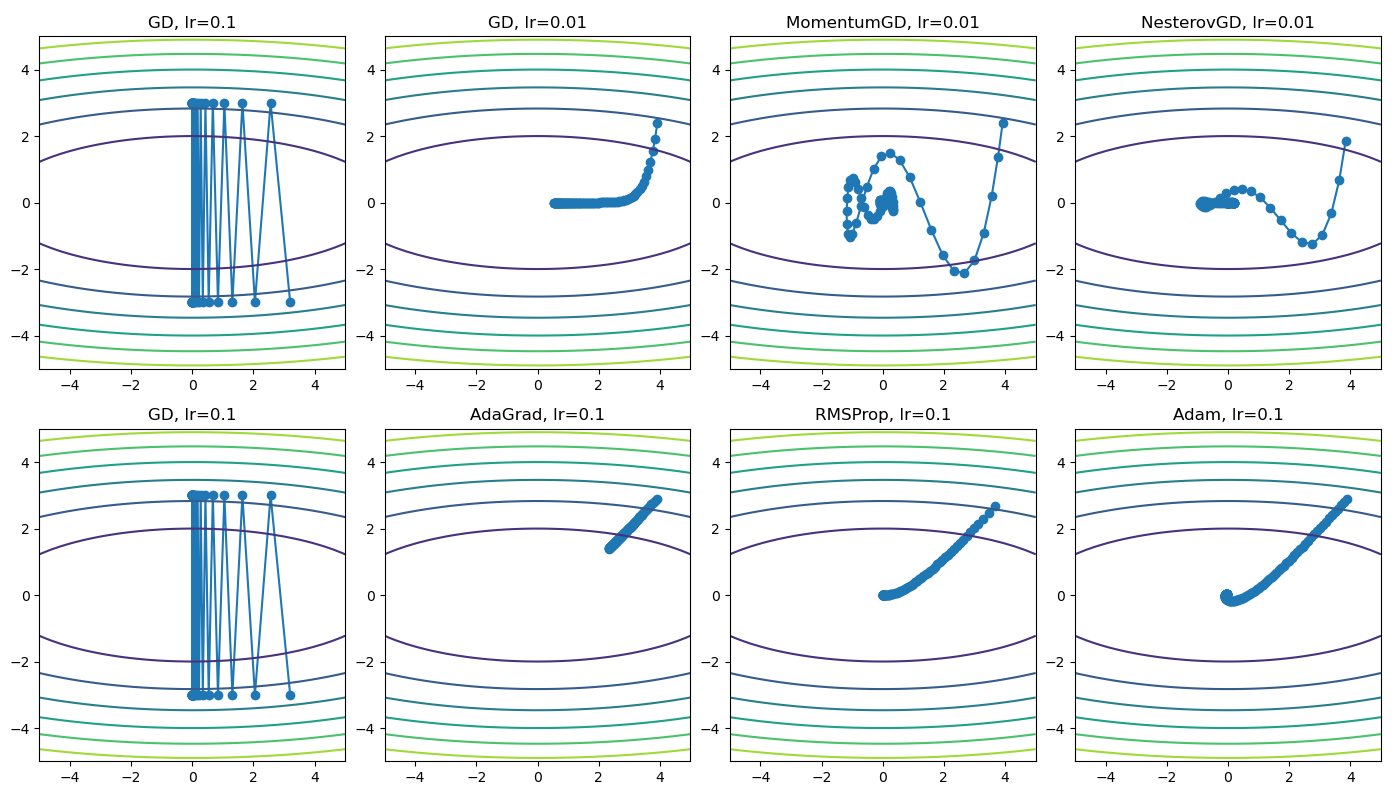
我们使用\(f(x_1, x_2) = x_1^2 + 10 x_2^2\)对各个算法进行测试并进行可视化,其结果如下所示。可以看到,当梯度下降的学习率过大时,参数无法收敛;当学习率过小时,收敛较慢。带动量的梯度下降和Nesterov GD通过引入动量项,加速了收敛。AdaGrad和RMSProp通过自适应学习率,使不同维度的收敛速度相近,从而也达到了加速收敛的目的。Adam算法则同时包含动量法和自适应学习率的优势,在这个问题中的表现最好。
至此,我们已经完成了从最基础的梯度下降到集大成者 Adam 的优化器实现之旅。希望通过手动编写这些算法,你能更深刻地理解每个优化器背后的核心思想:
- 梯度下降 (GD):通过梯度负方向实现最基本的参数更新。
- 带动量的梯度下降/Nesterov:引入“动量”项,加速收敛并减少震荡。
- Adagrad/RMSProp:引入自适应学习率,为每个参数定制更新步长,有效处理不同参数的更新需求。
- Adam:结合了动量和自适应学习率的优势,成为目前最常用、最稳定的优化算法之一。
手动实现这些优化器不仅仅是代码练习,更是一次深入理解深度学习优化原理的宝贵机会。当你下次在训练模型时,便不再是简单地调用 .step(),而是能清晰地感知到参数更新背后那套精妙的数学机制。
以下程序完整代码。
import numpy as np
import torch
from matplotlib import pyplot as plt
class GD:
def __init__(self, x, lr=0.01):
self.x = x
self.lr = lr
def step(self):
with torch.no_grad():
self.x -= self.lr * self.x.grad
def zero_grad(self):
self.x.grad.zero_()
class MomentumGD:
def __init__(self, x, lr=0.01, momentum=0.9):
self.x = x
self.lr = lr
self.momentum = momentum
self.v = torch.zeros_like(x)
def step(self):
with torch.no_grad():
self.v = self.momentum * self.v + self.x.grad
self.x -= self.lr * self.v
def zero_grad(self):
self.x.grad.zero_()
class NesterovGD:
def __init__(self, x, lr=0.01, momentum=0.9):
self.x = x
self.lr = lr
self.momentum = momentum
self.v = torch.zeros_like(x)
def step(self):
with torch.no_grad():
self.v = self.momentum * self.v + self.x.grad
self.x -= self.lr * (self.x.grad + self.momentum * self.v)
def zero_grad(self):
self.x.grad.zero_()
class AdaGrad:
def __init__(self, x, lr=0.01, eps=1e-8):
self.x = x
self.lr = lr
self.h = torch.zeros_like(x)
self.eps = eps
def step(self):
with torch.no_grad():
self.h += self.x.grad ** 2
self.x -= self.lr * self.x.grad / (self.h + self.eps) ** 0.5
def zero_grad(self):
self.x.grad.zero_()
class RMSProp:
def __init__(self, x, lr=0.01, alpha=0.9, eps=1e-8):
self.x = x
self.lr = lr
self.h = torch.zeros_like(x)
self.alpha = alpha
self.eps = eps
def step(self):
with torch.no_grad():
self.h = self.alpha * self.h + (1 - self.alpha) * self.x.grad ** 2
self.x -= self.lr * self.x.grad / (self.h + self.eps) ** 0.5
def zero_grad(self):
self.x.grad.zero_()
class Adam:
def __init__(self, x, lr=0.01, beta1=0.9, beta2=0.999, eps=1e-8):
self.x = x
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.eps = eps
self.v = torch.zeros_like(x)
self.h = torch.zeros_like(x)
self.t = 0
def step(self):
self.t += 1
with torch.no_grad():
self.v = self.beta1 * self.v + (1 - self.beta1) * self.x.grad
self.h = self.beta2 * self.h + (1 - self.beta2) * self.x.grad ** 2
v_hat = self.v / (1 - self.beta1 ** self.t)
h_hat = self.h / (1 - self.beta2 ** self.t)
self.x -= self.lr * v_hat / (h_hat.sqrt() + self.eps)
def zero_grad(self):
self.x.grad.zero_()
def fun(x):
return x[0] ** 2 + 10 * x[1] ** 2
def test(optimizer, x):
MAX_ITER = 100
res = []
for i in range(MAX_ITER):
y = fun(x)
y.backward()
optimizer.step()
optimizer.zero_grad()
res.append(x.detach().numpy().copy())
res = np.array(res)
plt.plot(res[:, 0], res[:, 1], 'o-')
xx = np.linspace(-5, 5, 100)
yy = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(xx, yy)
Z = fun(np.array([X, Y]))
plt.contour(X, Y, Z)
def main():
plt.figure(figsize=(16, 8))
x = torch.tensor([4.0, 3.0], requires_grad=True)
plt.subplot(2, 4, 1)
optimizer = GD(x, lr=0.1)
test(optimizer, x)
plt.title('GD, lr=0.1')
x = torch.tensor([4.0, 3.0], requires_grad=True)
plt.subplot(2, 4, 2)
optimizer = GD(x, lr=0.01)
test(optimizer, x)
plt.title('GD, lr=0.01')
x = torch.tensor([4.0, 3.0], requires_grad=True)
plt.subplot(2, 4, 3)
optimizer = MomentumGD(x, lr=0.01)
test(optimizer, x)
plt.title('MomentumGD, lr=0.01')
x = torch.tensor([4.0, 3.0], requires_grad=True)
plt.subplot(2, 4, 4)
optimizer = NesterovGD(x, lr=0.01)
test(optimizer, x)
plt.title('NesterovGD, lr=0.01')
x = torch.tensor([4.0, 3.0], requires_grad=True)
plt.subplot(2, 4, 5)
optimizer = GD(x, lr=0.1)
test(optimizer, x)
plt.title('GD, lr=0.1')
x = torch.tensor([4.0, 3.0], requires_grad=True)
plt.subplot(2, 4, 6)
optimizer = AdaGrad(x, lr=0.1)
test(optimizer, x)
plt.title('AdaGrad, lr=0.1')
x = torch.tensor([4.0, 3.0], requires_grad=True)
plt.subplot(2, 4, 7)
optimizer = RMSProp(x, lr=0.1)
test(optimizer, x)
plt.title('RMSProp, lr=0.1')
x = torch.tensor([4.0, 3.0], requires_grad=True)
plt.subplot(2, 4, 8)
optimizer = Adam(x, lr=0.1)
test(optimizer, x)
plt.title('Adam, lr=0.1')
plt.tight_layout()
plt.show()
if __name__ == '__main__':
main()
本文总阅读量次