一个和投影有关的问题的解答

第一问，注意到\(\nabla_x f(x) = -2(z - x)\)即可。

第二问，先证明，对任意\(x\in\mathcal{X}\)，\(x + x^* \in\mathcal{X}\)，因此\((z - x^*)^T x = (z - x^*)^T(x + x^* - x^*)\leq 0\)。然后，对于任意\(x\in\mathcal{X}\)，$-x\in\mathcal{X}$，因此\((z - x^*)^Tx = -(z - x^*)^T(-x)\geq 0\)。那么只能有\((z - x^*)^Tx = 0\)。实际上，这一问的几何意义非常明显，就是向量与其投影的残差是子空间的法向量。

第三问，因为\(P_{\mathcal{X}}(y)\in \mathcal{X}\)，根据第一问，有\((x - P_{\mathcal{X}}(x))^T(P_{\mathcal{X}}(y) - P_{\mathcal{X}}(x))\leq 0\)。同理，\((y - P_{\mathcal{X}}(y))^T(P_{\mathcal{X}}(x) - P_{\mathcal{X}}(y))\leq 0\)。因此

\[(P_{\mathcal{X}}(y) - P_{\mathcal{X}}(x))^T(y - P_{\mathcal{X}}(y) - x + P_{\mathcal{X}}(x)) \geq 0\]

从而

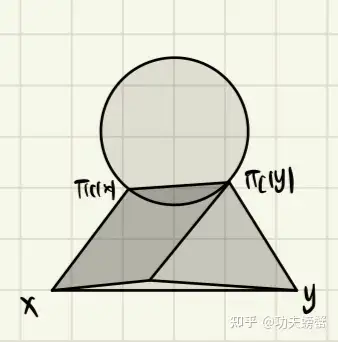
\[\begin{aligned} \|y - x\|^2 &= \|y - P_{\mathcal{X}}(y) + x - P_{\mathcal{X}}(x) + P_{\mathcal{X}}(y) - P_{\mathcal{X}}(x)\|^2\\ &= \|P_{\mathcal{X}}(y) - P_{\mathcal{X}}(x)\|^2 + \|y - P_{\mathcal{X}}(y) + x - P_{\mathcal{X}}(x)\|^2 + 2(P_{\mathcal{X}}(y) - P_{\mathcal{X}}(x))^T(y - P_{\mathcal{X}}(y) + x - P_{\mathcal{X}}(x))\\ &\geq 0 \\ \end{aligned}\]

画个示意图可能更能看出来证明的思路